已知a,b,c为正数,且满足abc=1.证明:
(1) ;
(2) .
((本小题满分10分)
已知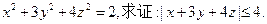
((本小题满分10分)
已知椭圆的参数方程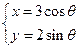 (
(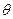 为参数),求椭圆上的动点P到直线
为参数),求椭圆上的动点P到直线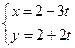 (t为参数)的最短距离。
(t为参数)的最短距离。
((本小题满分10分)
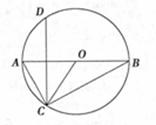
如图,在⊙O中,弦CD垂直于直径AB,求证: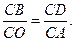
(.(本小题满分12分)
已知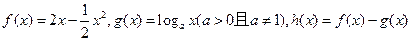 在定义域上为减函数,且其导函数
在定义域上为减函数,且其导函数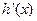 存在零点。
存在零点。
(I)求实数a的值;
(II)函数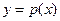 的图象与函数
的图象与函数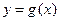 的图象关于直线y=x对称,且
的图象关于直线y=x对称,且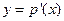 为函数
为函数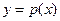 的导函数,
的导函数,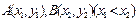 是函数
是函数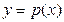 图像上两点,若
图像上两点,若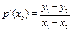 ,判断
,判断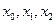 的大小,并证明你的结论。
的大小,并证明你的结论。
((本小题满分12分)
已知F1、F2分别是椭圆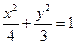 的左、右焦点,曲线C是坐标原点为顶
的左、右焦点,曲线C是坐标原点为顶 点,
点, 以F2为焦点的抛物线,过点F1的直线
以F2为焦点的抛物线,过点F1的直线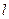 交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
(I)求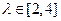 ,求直线
,求直线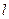 的斜率k的取值范围;
的斜率k的取值范围;
(II)求证:直线MQ过定点。