如图,已知多面体ABC-A 1B 1C 1,A 1A,B 1B,C 1C均垂直于平面ABC,∠ABC=120°,A 1A=4,C 1C=1,AB=BC=B 1B=2.

(Ⅰ)证明:AB 1⊥平面A 1B 1C 1;
(Ⅱ)求直线AC 1与平面ABB 1所成的角的正弦值.
3个同学分别从a,b,c,d四门校本课程中任选其中一门,每个同学选哪一门互不影响;(I)求3个同学选择3门不同课程的概率;(II)求恰有2门课程没有被选择的概率;(Ⅲ)求选择课程a的同学个数的分布列及数学期望.
从甲地到乙地一天共有A、B 两班车,由于雨雪天气的影响,一段时间内A 班车正点到达乙地的概率为0.7,B 班车正点到达乙地的概率为0.75。
(1)有三位游客分别乘坐三天的A 班车,从甲地到乙地,求其中恰有两名游客正点到达的概率(答案用小数表示)。
(2)有两位游客分别乘坐A、B 班车,从甲地到乙地,求其中至少有1 人正点到达的概率(答案用小数表示)。
已知极坐标系的极点在直角坐标系的原点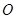 处,极轴与
处,极轴与 轴的正半轴重合.直线
轴的正半轴重合.直线 的参数方程为
的参数方程为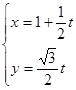 (
(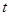 为参数),圆
为参数),圆 的极坐标方程为
的极坐标方程为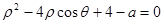 .若直线
.若直线 与圆
与圆 相交于
相交于 、
、 且
且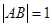 ,求实数
,求实数 的值.
的值.
在平面直角坐标系xOy中,设圆C: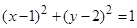 在矩阵
在矩阵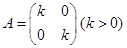 对应的线性变换下得到曲线F所围图形的面积为
对应的线性变换下得到曲线F所围图形的面积为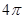 ,求
,求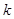 的值
的值
已知函数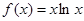 ,
,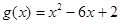 。
。
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数 在区间
在区间
 上的最小值;
上的最小值;
(Ⅲ)试判断方程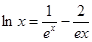 (其中
(其中 )是否有实数解?并说明理由。
)是否有实数解?并说明理由。