设an是等比数列，公比大于0，其前n项和为Snn∈N，bn是-优题课

题文

设 $\{a_{n}\}$ 是等比数列，公比大于0，其前n项和为 $S_{n} (n \in N^{*})$ ， $\{b_{n}\}$ 是等差数列.已知 $a_{1} = 1$ ， $a_{3} = a_{2} + 2$ ， $a_{4} = b_{3} + b_{5}$ ， $a_{5} = b_{4} + 2 b_{6}$ .

（I）求 $\{a_{n}\}$ 和 $\{b_{n}\}$ 的通项公式；

（II）设数列 $\{S_{n}\}$ 的前n项和为 $T_{n} (n \in N^{*})$ ，

（i）求 $T_{n}$ ；

（ii）证明 $\sum_{k = 1}^{n} \frac{(T_{k} + b_{k + 2}) b_{k}}{(k + 1) (k + 2)} = \frac{2^{n + 2}}{n + 2} - 2 (n \in N^{*})$ .

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

已知函数是常数且）在区间上有
（1）求的值；
（2）若当时，求的取值范围；

已知集合
（1）能否相等？若能，求出实数的值，若不能，试说明理由？
（2）若命题命题且是的充分不必要条件，求实数的取值范围；

已知且
（1）求的值；
（2）求的值；

已知幂函数的图象与x轴，y轴无交点且关于原点对称，又有函数f(x)=x²－alnx+m－2在(1，2]上是增函数，g(x)=x－在(0,1)上为减函数.
①求a的值；
②若，数列{a_n}满足a₁＝1，a_n+1＝p(a_n)，（n∈N₊），数列{b_n}，满足，，求数列{a_n}的通项公式a_n和s_n.
③设，试比较[h(x)]ⁿ+2与h(xⁿ)+2ⁿ的大小（n∈N₊），并说明理由.

已知二次函数h(x)=ax²+bx+c(其中c<3)，其导函数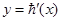的图象如图，f(x)=6lnx+h(x).

①求f(x)在x=3处的切线斜率；
②若f(x)在区间(m,m+)上是单调函数，求实数m的取值范围；
③若对任意k∈[-1,1]，函数y=kx(x∈(0,6])的图象总在函数y＝f(x)图象的上方，求c的取值范围.

试卷网试题网古诗词网作文网范文网