如图,在三棱柱 ABC−
中,
平面 ABC, D, E, F, G分别为
, AC,
,  的中点, AB=BC=
, AC=
=2.
的中点, AB=BC=
, AC=
=2.

(1)求证: AC⊥平面 BEF;
(2)求二面角 B−CD− C 1的余弦值;
(3)证明:直线 FG与平面 BCD相交.
我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径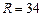 百公里)的中心
百公里)的中心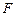 为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)
为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)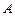 到火星表面的距离为
到火星表面的距离为 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点)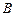 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点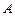 第一次逆时针运行到与轨道中心
第一次逆时针运行到与轨道中心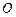 的距离为
的距离为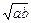 百公里时进行变轨,其中
百公里时进行变轨,其中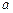 、
、 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).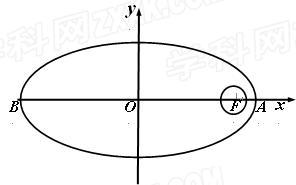
已知动点(x, y) 在曲线C上,将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程 ;定点M(2,1),平行于OM的直线
;定点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.
(1)求曲线 的方程; (2)求m的取值范围.
的方程; (2)求m的取值范围.
已知:以点C (t, )(t∈R , t≠ 0) 为圆心的圆与
为圆心的圆与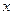 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.
求过两直线l1:x+y+1=0与l2:5x-y-1=0的交点,且与直线3x+2y+1=0的夹角为45o的直线的方程.
已知数列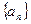 中,
中,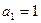 ,且
,且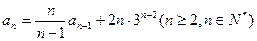 .
.
(1)求数列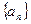 的通项公式
的通项公式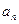 ;
;
(2)令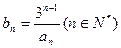 ,数列
,数列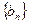 的前
的前 项和为
项和为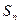 ,试比较
,试比较 与
与 的大小;
的大小;
(3)令 ,数列
,数列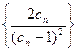 的前
的前 项和为
项和为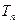 ,求证:对任意
,求证:对任意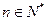 ,都有
,都有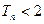 .
.