电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 |
第一类 |
第二类 |
第三类 |
第四类 |
第五类 |
第六类 |
电影部数 |
140 |
50 |
300 |
200 |
800 |
510 |
好评率 |
0.4 |
0.2 |
0.15 |
0.25 |
0.2 |
0.1 |
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
假设所有电影是否获得好评相互独立.
(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率;
(Ⅲ)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用" "表示第 k类电影得到人们喜欢," "表示第 k类电影没有得到人们喜欢( k=1,2,3,4,5,6).写出方差 , , , , , 的大小关系.
某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利;(2)若干年后,有两种处理方案:
方案一:年平均获利最大时,以26万元出售该渔船;
方案二:总纯收入获利最大时,以8万元出售该渔船.问哪种方案合算?
已知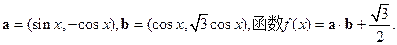
(1)求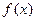 的最小正周期,并求其图象对称中心的坐标;
的最小正周期,并求其图象对称中心的坐标;
(2)当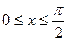 时,求函数
时,求函数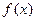 的值域。
的值域。
已知A、B是抛物线y2=2px(p>0)上的两点,且满足OA⊥OB(O为坐标原点).
求证:(1)A、B两点的横坐标之积、纵坐标之积分别为定值;(2)直线AB经过一个定点.
已知椭圆 ,是否存在斜率为k(k≠0)的直线
,是否存在斜率为k(k≠0)的直线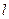 ,使
,使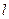 与椭圆交于不同的两点A、B,且线段
与椭圆交于不同的两点A、B,且线段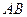 的垂直平分线经过点M(0,-1),求斜率k的取值范围.
的垂直平分线经过点M(0,-1),求斜率k的取值范围.
中心在坐标原点,焦点在x轴上的椭圆,它的离心率为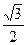 ,与直线x+y-1=0相交于两点M、N,且以
,与直线x+y-1=0相交于两点M、N,且以 为直径的圆经过坐标原点.求椭圆的方程.
为直径的圆经过坐标原点.求椭圆的方程.