如图,在正方形 , 分别在边 上(不与端点重合),且 ,过D点作 , 垂足为F.

(1)证明: 四点共圆;
(2)若 ,E为DA的中点,求四边形BCGF的面积.
(满分12分)
已知曲线 在第三象限
在第三象限
(1)求P0的坐标;
(2)若直线 的方程。
的方程。
已知数列
 中,
中, ,
, 且
且 ,其前
,其前 项和为
项和为 ,且当
,且当 时,
时, .
.
⑴求证:数列 是等比数列;
是等比数列;
⑵求数列 的通项公式;
的通项公式;
⑶若 ,令
,令 ,记数列
,记数列 的前
的前 项和为
项和为 .设
.设
 是整数,问是否存在正整数
是整数,问是否存在正整数 ,使等式
,使等式 成立?若存在,求出
成立?若存在,求出 和相应的
和相应的 值;若不存在,请说明理由.
值;若不存在,请说明理由.
已知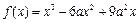 (
( ).
).
⑴求函数 的单调递减区间;
的单调递减区间;
⑵当 时,若对
时,若对 有
有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
三棱柱 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
,  分别是
分别是 ,
,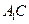 的中点.
的中点.
⑴求证: 平面
平面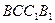 ;
;
⑵求证: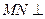 平面
平面 ;
;
⑶求二面角 的余弦值.
的余弦值.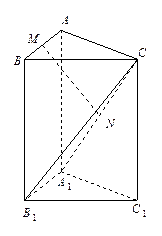
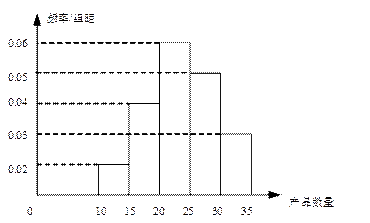
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为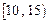 ,
,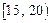 ,
,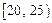 ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
⑴求 ;
;
⑵工厂规定从各组中任选1人进行再培训,则选取5人不在同一组的概率是多少?