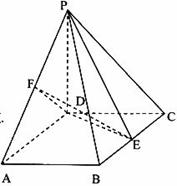
在平行四边形 中,

求证:
(1) 平面
(2)平面 平面
.(本小题满分14分)
已知数列 是首项为
是首项为 ,公差为
,公差为 的等差数列,
的等差数列, 是首项为
是首项为 ,公比为
,公比为 的等比数列,且满足
的等比数列,且满足 ,其中
,其中 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若数列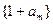 与数列
与数列 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列 ,求数列
,求数列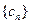 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列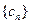 的前项之和为
的前项之和为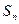 ,求证:
,求证: .
.
(本小题满分14分)
设椭圆 的左右焦点分别为
的左右焦点分别为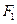 、
、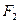 ,
, 是椭圆
是椭圆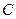 上的一点,
上的一点,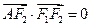 ,坐标原点
,坐标原点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆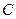 的方程;
的方程;
(2)设 是椭圆
是椭圆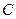 上的一点,过点
上的一点,过点 的直线
的直线 交
交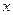 轴于点
轴于点 ,交
,交 轴于点
轴于点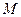 ,若
,若 ,求直线
,求直线 的斜率.
的斜率.
(本小题满分14分)
设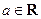 ,函数
,函数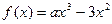
(Ⅰ)若 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若函数 在
在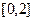 上是单调减函数,求实数
上是单调减函数,求实数 的取值范围.
的取值范围.
(本小题满分14分)
如图,四棱锥 的底面
的底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 、
、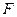 分别为
分别为 、
、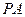 的中点。
的中点。
(I)求证: 平面
平面 ;
; (Ⅱ)求三棱锥
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ)求平面 与平面
与平面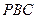 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。
(本小题满分12分)
某菜园要将一批蔬菜用汽车从所在城市甲运至亚运村乙,已知从城市甲到亚运村乙只有两条公路,且运费由菜园承担.
若菜园恰能在约定日期( 月
月 日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提
日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提 前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.
前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.
为保证蔬菜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送蔬菜,已知下表内的信息:
| 统计信息 汽车行 驶路线 |
不堵车的情况下到达亚运村乙所需时间 (天) |
堵车的情况下到达亚运村乙所需时间 (天) |
堵车的 概率 |
运费 (万元) |
| 公路1 |
2 |
3 |
 |
 |
| 公路2 |
1 |
4 |
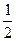 |
 |
(注:毛利润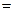 销售商支付给菜园的费用
销售商支付给菜园的费用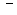 运费)
运费)
(Ⅰ) 记汽车走公路1时菜园获得的毛利润为 (单位:万元),求
(单位:万元),求 的分布列和数学期望
的分布列和数学期望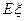 ;
;
(Ⅱ) 假设你是菜园的决策者,你选择哪条公路运送蔬菜有可能让菜园获得的毛利润更多?