如图，直三棱柱ABC﹣A 1B 1C 1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA 1的长为5．
（1）求三棱柱ABC﹣A 1B 1C 1的体积；
（2）设M是BC中点，求直线A 1M与平面ABC所成角的大小.
【原创】设
，其中
．
（1）若
无极值，求
的取值范围；
（2）若当
，
恒成立，求的取值范围．
已知函数
，其中
（Ⅰ）求
在
上的单调区间；
（Ⅱ）求在
（
为自然对数的底数）上的最大值；
（Ⅲ）对任意给定的正实数
，曲线
上是否存在两点
、
，使得
是以原点
为直角顶点的直角三角形，且此三角形斜边中点在
轴上？
已知
，命题
：对任意
，不等式
恒成立；命题
：存在
，使得
成立
（Ⅰ）若为真命题，求
的取值范围；
（Ⅱ）当
，若且为假，或为真，求的取值范围。
（Ⅲ）若
且是的充分不必要条件，求
的取值范围。
已知
，求证：关于
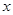的三个方程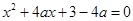
，
，
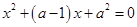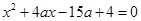中至少有一个方程有实数根.
已知复数z1＝m（m－1）＋（m－1）i是纯虚数．
（1）求实数m的值；
（2）若（3＋z1）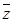
＝4＋2i，求复数z．