（1）发现：如图①所示，在正方形ABCD中，E为AD边上一点-优题课

题文

（1）发现：如图①所示，在正方形 $A B C D$ 中， $E$ 为AD边上一点，将 $△ A E B$ 沿 $B E$ 翻折到 $△ B E F$ 处，延长 $E F$ 交 $C D$ 边于 $G$ 点．求证： $△ B F G ≌ △ B C G$ ；

（2）探究：如图②，在矩形 $A B C D$ 中， $E$ 为 $A D$ 边上一点，且 $A D ＝ 8 ， A B ＝ 6$ ．将 $△ A E B$ 沿 $B E$ 翻折到 $△ B E F$ 处，延长 $E F$ 交 $B C$ 边于 $G$ 点，延长 $B F$ 交 $C D$ 边于点 $H$ ，且 $F H ＝ C H$ ，求 $A E$ 的长．

（3）拓展：如图③，在菱形 $A B C D$ 中， $A B ＝ 6$ ， $E$ 为 $C D$ 边上的三等分点， $∠ D ＝ 60 °$ ．将 $△ A D E$ 沿 $A E$ 翻折得到 $△ A F E$ ，直线 $E F$ 交 $B C$ 于点 $P$ ，求 $P C$ 的长．

科目数学题型解答题难度较难

登录免费查看答案和解析

相关试题

（内江）如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且圆的直径AB在线段AE上．

（1）试说明CE是⊙O的切线；
（2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；
（3）设点D是线段AC上任意一点（不含端点），连接OD，当CD+OD的最小值为6时，求⊙O的直径AB的长．

（内江）如图，抛物线与x轴交于点A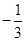（，0）、点B（2，0），与y轴交于点C（0，1），连接BC．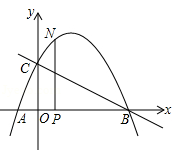

（1）求抛物线的函数关系式；
（2）点N为抛物线上的一个动点，过点N作NP⊥x轴于点P，设点N的横坐标为t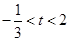（），求△ABN的面积S与t的函数关系式；
（3）若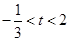且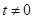时△OPN∽△COB，求点N的坐标．

（达州）化简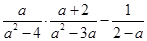，并求值，其中a与2、3构成△ABC的三边，且a为整数．

（达州）学习“利用三角函数测高”后，某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB，其测量步骤如下：

（1）在中心广场测点C处安置测倾器，测得此时山顶A的仰角∠AFH=30°；
（2）在测点C与山脚B之间的D处安置测倾器（C、D与B在同一直线上，且C、D之间的距离可以直接测得），测得此时山顶上红军亭顶部E的仰角∠EGH=45°；
（3）测得测倾器的高度CF=DG=1.5米，并测得CD之间的距离为288米；
已知红军亭高度为12米，请根据测量数据求出凤凰山与中心广场的相对高度AB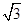．（取1.732，结果保留整数）

（南充）如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．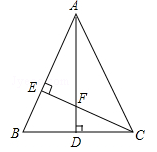

求证：（1）△AEF≌△CEB；
（2）AF=2CD．

试卷网试题网古诗词网作文网范文网