已知在 中, , 四边形 是正方形,连接 是 的中点.

(1)如图①,当 在一条直线上时,试判断 与 的位置关系,并求 的值;
(2)如图②,当 绕点 旋转后,(1)中结论是否仍然成立?试说明理由.
九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
| 时间x(天) |
1≤x<50 |
50≤x≤90 |
| 售价(元/件) |
x+40 |
90 |
| 每天销量(件) |
200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
为了考察冰川融化的状况,一支科考队在某冰川上设定一个以大本营O为圆心,半径为4km 圆形考察区域,线段P1P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整数)的关系是 .以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).
.以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(-4,9)、(-13,-3).
(1)求线段P1P2所在的直线对应的函数关系式;
(2)求冰川的边界线移动到考察区域所需要的最短时间.
小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长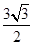 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.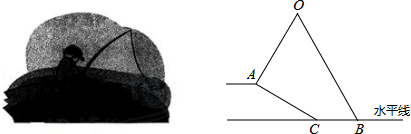
在一个不透明的口袋里装有分别标有数字﹣3、﹣1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率;
(2)从中任取一球,将球上的数字记为a,求关于x的一元二次方程ax2﹣2ax+a+3=0有实数根的概率;
(3)从中任取一球,将球上的数字作为点的横坐标记为x(不放回);再任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
无锡市对初三年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三种成绩共1000份进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如下表及图所示.
 |
A |
B |
C |
D |
| 物理实验操作 |
120 |
a70 |
90 |
20 |
| 化学实验操作 |
90 |
110 |
30 |
c 7020 |
| 体育 |
b70123 |
140 |
160 |
18 |
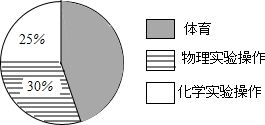
(1)请将上表补充完整(直接填数据,不写解答过程).
(2)无锡市共有40000名学生参加测试,试估计该市初三年级学生化学实验操作合格及合格以上大约有多少人?
(3)在这40000名学生中,体育成绩不合格的大约有多少人?