设直角三角形的两条直角边长分别为 斜边长为 若 均为正数，且 ，求满足条件的直角三角形的个数.
（本题满分6分，）小明有5张写着不同的数字的卡片，请你按要求抽出卡片，完成下面各题：
（1）从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少？
（2）从中取出4张卡片，用学过的运算方法，使结果为24．如何抽取？写出运算式子（一种即可）
答：（1）我抽取的2张卡片是____________ 、____________ 、
乘积的最大值为____________ ．
（2）我抽取的4张卡片是___________ 、____________ 、___________ 、____________ ，
算24的式子为__________________________________________．
（本题14分）如图，在平面直角坐标系中，抛物线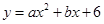
经过点A（-3，0）和点B（2，0）．直线y=h（h为常数，且0＜h＜6）与BC交于点D，与y轴交于点E，与AC交于点F，与抛物线在第二象限交于点G．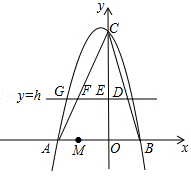
（1）求抛物线的解析式；
（2）连接BE，求h为何值时，△BDE的面积最大；
（3）已知一定点M（-2，0）．问：是否存在这样的直线y=h，使△OMF是等腰三角形？若存在，请求出h的值和点G的坐标；若不存在，请说明理由．
（本题12分）某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，假设每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球运行时，设乒乓球与端点A的水平距离为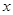
（米），与桌面的高度为
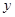（米），运行时间为
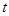（秒），经多次测试后，得到如下部分数据：2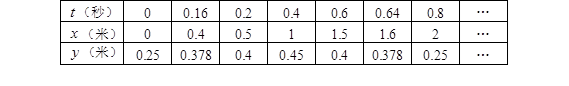
（1）当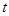为何值时，乒乓球达到最大高度？
（2）乒乓球落在桌面时，与端点A的水平距离是多少？
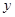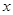（3）乒乓球落在桌面上弹起后，与满足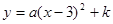
．
①用含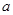
的代数式表示
；
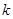②球网高度为0.14米，球桌长（1.4×2）米，若球弹起后，恰好有唯一的击球点，可以将球沿直线扣杀到点A，求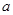的值．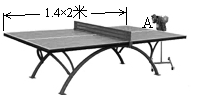
（本题12分）如图，抛物线
与x轴交于A、B两点，与y轴交于C点．
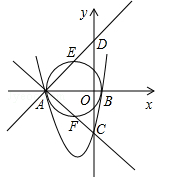
（1）求抛物线的顶点坐标；
（2）设直线
与y轴的交点是D，在线段AD上任意取一点E（不与A、D重合），经过A、B、E三点的圆交直线AC于点F，试判断△BEF的形状，并说明理由．
（本题10分）某商品的进价为每件30元，现在的售价为每件40元，每星期可卖出150件．市场调查反映：如果每件的售价每涨1元（售价每件不能高于45元），那么每星期少卖10件．设每件涨价x元（x为非负整数），每星期的销量为y件．
（1）求y与x的函数关系式及自变量x的取值范围；
（2）如何定价才能使每星期的利润最大且每星期的销量较大？每星期的最大利润是多少？