我们用部分自然数构造如下的数表：用aij(i≥j)表示第i行第j个数(i、j为正整数)，使ail=aii="i" ；每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外，如图)，设第n(n为正整数)行中各数之和为bn．
（1）试写出b2一2b1；，b3-2b2，b4-2b3,b5-2b4，并推测bn+1和bn的关系(无需证明)；
（2）证明数列{bn+2}是等比数列，并求数列{bn}的通项公式bn；
（3）数列{ bn}中是否存在不同的三项bp，bq，br(p，q，r为正整数)恰好成等差数列?若存在求出P，q，r的关系；若不存在，请说明理由．
 |
命题
：方程
有两个不等的正实数根，命题
：函数
在R上是减函数.若“或”为真命题，“且” 为假命题，求
的取值范围.
一个容量为M的样本数据，其频率分布表如下．
（Ⅰ）完成频率分布表 ；
（Ⅱ）画出频率分布直方图 ；
（Ⅲ）利用频率分布直方图，估计总体的众数、中位数及平均数．
【解】 频率分布表频率分布直方图
| 分组 |
频数 |
频率 |
| (10,20] |
2 |
0.10 |
| (20,30] |
3 |
|
| (30,40] |
4 |
0.20 |
| (40,50] |
||
| (50,60] |
4 |
0.20 |
| (60,70] |
2 |
0.10 |
| 合计 |
1.00 |
已知函数
（1）当
=
时，求曲线
在点（
,
）处的切线方程。
(2)若函数在（1，）上是减函数，求实数的取值范围；
（3）是否存在实数
若不存在，说明理由。若存在，求出的值，并加以证明。
已知椭圆的中心是坐标原点
，焦点在
轴上，离心率为
，又椭圆上任一点到两焦点的距离和为
．过右焦点
与轴不垂直的直线
交椭圆于
，
两点。
（1）求椭圆的方程；
（2）在线段
上是否存在点
,使得
？若存在，求出
的取值范围；若不存在，请说明理由.
如图示，边长为4的正方形
与正三角形
所在平面互相垂直，M、Q分别是PC，AD的中点。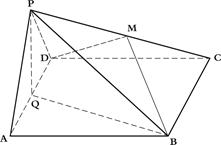
（1）求证： 
（2）求多面体
的体积
（3）试问：在线段AB上是否存在一点N，使面
若存在，指出N的位置，若不存在，请说明理由。