已知 ,直线
,直线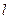 与函数
与函数 的图象都相切于点
的图象都相切于点 。
。
(1)求直线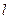 的方程及
的方程及 的解析式;
的解析式;
(2)若 (其中
(其中 是
是 的导函数),求函数
的导函数),求函数 的极大值.
的极大值.
已知向量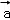 =(1,2),
=(1,2),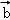 =(2,2).
=(2,2).
(1)求(2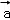 ﹣
﹣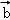 )•(2
)•(2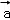 +
+ );
);
(2)设 =(﹣3,λ),若
=(﹣3,λ),若 与
与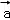 夹角为钝角,求λ的值.
夹角为钝角,求λ的值.
已知函数f(x)=2sinxcosx﹣2sin2x+1.
(1)x∈[0, ],求函数f(x)的值域;
],求函数f(x)的值域;
(2)x∈[0,π],求f(x)的单调递增区间.
已知向量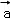 与
与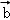 的夹角为60°,|
的夹角为60°,| |=1,|
|=1,|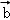 |=2
|=2
(1)求(2 ﹣
﹣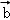 )•
)• ;
;
(2)求:|2 +
+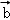 |.
|.
已知函数f(x)=log2 +log2(x﹣1)+log2(p﹣x).
+log2(x﹣1)+log2(p﹣x).
(1)求函数f(x)的定义域;
(2)求函数f(x)的值域.
已知函数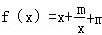 (x∈[1,+∞)且m<1).
(x∈[1,+∞)且m<1).
(Ⅰ)用定义证明函数f(x)在[1,+∞)上为增函数;
(Ⅱ)设函数 ,若[2,5]是g(x)的一个单调区间,且在该区间上g(x)>0恒成立,求实数m的取值范围.
,若[2,5]是g(x)的一个单调区间,且在该区间上g(x)>0恒成立,求实数m的取值范围.