设函数f(x)=lnx-px+1(1)当 P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明:
P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明: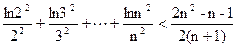 (n∈N
(n∈N ,n≥2)
,n≥2)
(本小题满分12分)某中学随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于小时的学生可申请在学校住宿,若招生 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(3)从学校的高一学生中任选4名学生,这4名学生中上学路上所需时间少于20分钟的人数记为 ,求
,求 的分布列和数学期望.(以直方图中的频率作为概率).
的分布列和数学期望.(以直方图中的频率作为概率).
(本小题满分12分)已知函数 满足
满足
(1)求实数 的值以及函数
的值以及函数 的最小正周期;
的最小正周期;
(2)记 ,若函数
,若函数 是偶函数,求实数
是偶函数,求实数 的值.
的值.
(本小题14分)已知函数 ,
,
(1)当 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)这直线 是曲线
是曲线 的切线,若
的切线,若 的斜率存在最小值
的斜率存在最小值 ,求
,求 的值,并求取得最小斜率时切线
的值,并求取得最小斜率时切线 的方程;
的方程;
(3)已知 分别在
分别在 处取得极值,求证:
处取得极值,求证: .
.
(本小题14分)椭圆 的两焦点坐标分别为
的两焦点坐标分别为 和
和 ,且
,且 过点
过点 .
.
(1)求椭圆方程;
(2)过点 作不与
作不与 轴垂直的直线
轴垂直的直线 交该椭圆于
交该椭圆于 两点,
两点, 为椭圆的左顶点.试猜想
为椭圆的左顶点.试猜想 的大小是否为定值,定值为多少?如果是定值,请证明;如果不是,请说明理由.
的大小是否为定值,定值为多少?如果是定值,请证明;如果不是,请说明理由.
(本小题12分)如图所示,一个直径 的半圆,过点
的半圆,过点 作这个圆所在平面的垂线,在垂线上取一点
作这个圆所在平面的垂线,在垂线上取一点 ,使
,使 ,
, 为半圆上的一个动点,
为半圆上的一个动点, 分别在
分别在 上,且
上,且 .
.
(1)证明: ;
;
(2)证明: 面
面 ;
;
(3)求三棱锥 体积的最大值.
体积的最大值.