（本大题满分14分）若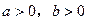
，且
，求
的最大值．
(本小题满分6分)
已知直线
与
的交点为
.
(Ⅰ)求交点
的坐标；
(Ⅱ)求过点且平行于
直线
的直线方程；
(Ⅲ)求过点且垂直于直线的直线方程.
已知函数
(
是常数)，且
，
.
(1) 求的值；
(2) 当
时，判断
的单调性
并证明；
(3) 对任意的
，若不等式
恒成立，求实数
的取值范围.
已知函数
(1) 若函数
的图象经过
（3，4）点，求
的值；
(2) 若
，求的值；
(3) 比较
大小，并写出比较过程.
某公司试销一种新产品，规定试销时销售单价不低于成本单价500元/件，又不高于800元/件，经试销调查，发现销售量
（件）与销售单价
（元/件）可近似看做一次函数
的关系（图象如下图所示）．
（1）根据图象，求一次函数的表达式；
（2）设公司获得的毛利润（毛利润＝销售总价－成本总价）为
元,
① 求关于的函数表达式；
② 求该公司可获得的最大毛利润，并求出此时相应的销售单价．
计算：（1）
；
（2） 
.