已知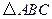 的顶点
的顶点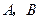 在椭圆
在椭圆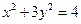 上,
上, 在直线
在直线 上,且
上,且 .
.
(1) 当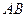 边通过坐标原点
边通过坐标原点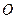 时,求
时,求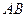 的长及
的长及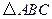 的面积;
的面积;
(2) 当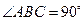 ,且斜边
,且斜边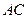 的长最大时,求
的长最大时,求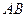 所在直线的方程.
所在直线的方程.
某学校成立三个社团,共60人参加,A社团有39人,B社团有33人,C社团有32人,同时只参加A、B社团的有10人,同时只参加A、C社团的有11人,三个社团都参加的有8人.随机选取一个成员.
(1)他至少参加两个社团的概率为多少?
(2)他参加不超过两个社团的概率为多少?
已知集合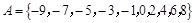 ,在平面直角坐标系中,点
,在平面直角坐标系中,点 的
的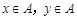 ,且
,且 ,计算
,计算
(1)点 不在x轴上的概率;
不在x轴上的概率;
(2)点 正好在第二象限的概率.
正好在第二象限的概率.
在箱子里装有10张卡片,分别写有1到10的10个数字,从箱子中任取一张卡片,记下它的读数x,然后再放回箱子中;第二次再从箱子中任意取出一张卡片,记下它的读数y.
求:(1) 是10的倍数的概率;
是10的倍数的概率;
(2)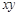 是3的倍数的概率.
是3的倍数的概率.
平面上画了一些彼此相距2a的平行线,把一枚半径r<a的硬币任意掷在这个平面上,求硬币不与任一条平行线相碰的概率.
一海豚在水池中自由游弋,水池为长30 m,宽20 m的长方形,求海豚嘴尖离岸边不超过2 m的概率.