设平面内的向量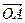（1，7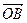），（5，1），（2，1），点P是直线-优题课

题文

设平面内的向量=（1，7），=（5，1），=（2，1），点P是直线OM上的一个动点，求当·取最小值时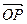，的坐标及ÐAPB的余弦值．

科目数学题型解答题难度较易

相关试题

（本题满分14分，第（1）、（2）小题各3分；第（3）、（4）小题各4分）
请你指出函数的基本性质（不必证明），并判断以下四个命题的正确性，必要时可直接运用有关其基本性质的结论加以证明．
（1）当时，等式恒成立；
（2）若，则一定有；
（3）若，方程有两个不相等的实数解；
（4）函数在上有三个零点．

（本题满分12分，第（1）小题5分，第（2）小题7分）
如图，是圆柱体的一条母线，已知过底面圆的圆心，是圆上不与点重合的任意一点，，，．

（1）求直线与直线所成角的大小；
（2）将四面体绕母线旋转一周，求的三边在旋转过程中所围成的几何体的体积．

（本题满分18分，第（1）小题4分，第（2）小题6分，第（3）小题8分）
我们把一系列向量按次序排成一列，称之为向量列，记作，已知向量列满足：，．
（1）证明：数列是等比数列；
（2）设，问数列中是否存在最小项？若存在，求出最小项；若不存在，请说明理由；
（3）设表示向量与间的夹角，若，对于任意正整数，不等式恒成立，求实数的范围．

（本题满分18分，第（1）小题4分，第（2）小题5分，第（3）小题9分）
设函数的定义域为，值域为，如果存在函数，使得函数的值域仍是，那么称是函数的一个等值域变换．
（1）判断下列函数是不是函数的一个等值域变换？说明你的理由；
，；
，．
（2）设函数的定义域为，值域为，函数的定义域为，值域为，那么“”是否为“是的一个等值域变换”的一个必要条件？请说明理由；
（3）设的定义域为，已知是的一个等值域变换，且函数的定义域为，求实数的值．