(本小题满分14分)已知二次函数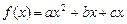 ,不等式
,不等式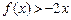 的解集为
的解集为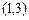 .(Ⅰ)若方程
.(Ⅰ)若方程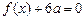 有两个相等的实根,求
有两个相等的实根,求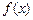 的解析式;(Ⅱ)若
的解析式;(Ⅱ)若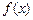 的最大值为正数,求实数
的最大值为正数,求实数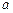 的取值范围.
的取值范围.
已知y=log4(2x+3-x2).
(1)求定义域;(2)求f(x)的单调区间;(3)求y的最大值,并求取最大值时x的值.
某学校共有高一、高二、高三学生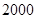 名,各年级男、女生人数如下图:
名,各年级男、女生人数如下图:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(Ⅰ)求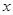 的值;
的值;
(Ⅱ)现用分层抽样的方法在全校抽取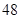 名学生,问应在高三年级抽取多少名?
名学生,问应在高三年级抽取多少名?
(Ⅲ)已知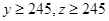 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.
已知集合 ,
,
(1)若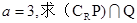 ;(2)若
;(2)若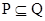 ,求实数
,求实数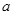 的取值范围.
的取值范围.
已知函数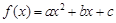 和函数
和函数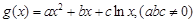 ,
,
(1)证明:只要 ,无论b取何值,函数
,无论b取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(2)在同一函数图象上任意取不同两点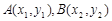 ,线段AB的中点为
,线段AB的中点为 ,记直线AB的斜率为
,记直线AB的斜率为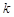 ,①对于函数
,①对于函数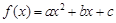 ,求证:
,求证: ;②对于函数
;②对于函数 ,是否具有与①同样的性质?证明你的结论.
,是否具有与①同样的性质?证明你的结论.
已知 是椭圆C:
是椭圆C: 与圆F:
与圆F: 的一个交点,且圆心F是椭圆的一个焦点,(1)求椭圆C的方程;(2)过F的直线交圆与P、Q两点,连AP、AQ分别交椭圆与M、N点,试问直线MN是否过定点?若过定点,则求出定点坐标;若不过定点,请说明理由.
的一个交点,且圆心F是椭圆的一个焦点,(1)求椭圆C的方程;(2)过F的直线交圆与P、Q两点,连AP、AQ分别交椭圆与M、N点,试问直线MN是否过定点?若过定点,则求出定点坐标;若不过定点,请说明理由.