设 ,函数
,函数 ,
, ,
, ,试讨论函数
,试讨论函数 的单调性.
的单调性.
设函数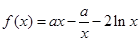 .
.
(1)若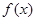 在
在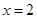 时有极值,求实数
时有极值,求实数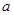 的值和
的值和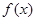 的极大值;
的极大值;
(2)若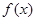 在定义域上是增函数,求实数
在定义域上是增函数,求实数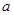 的取值范围.
的取值范围.
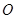 为坐标原点,已知向量
为坐标原点,已知向量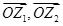 分别对应复数
分别对应复数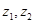 ,且
,且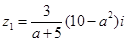 ,
,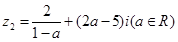 ,
,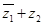 可以与任意实数比较大小,求
可以与任意实数比较大小,求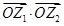 的值.
的值.
已知函数 在
在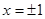 处取得极值,求函数
处取得极值,求函数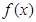 以及
以及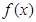 的极大值和极小值.
的极大值和极小值.
设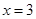 是函数
是函数 的一个极值点.
的一个极值点.
(1)求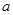 与
与 的关系式(用
的关系式(用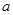 表示
表示 ),并求
),并求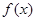 的单调区间;
的单调区间;
(2)设 ,
,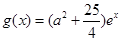 在区间[0,4]上是增函数.若存在
在区间[0,4]上是增函数.若存在 使得
使得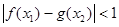 成立,求
成立,求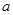 的取值范围.
的取值范围.
已知函数:f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1
(1)y=f(x)在x=-2时有极值,求f(x)的表达式;
(2)函数y=f(x)在区间[-2,1]上单调递增,求b的取值范围.