已知正项数列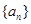 的前
的前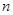 项和为
项和为 ,对任意
,对任意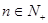 ,有
,有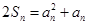 .
.
(1)求数列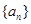 的通项公式;
的通项公式;
(2)令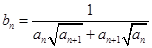 ,设
,设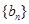 的前
的前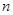 项和为
项和为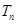 ,求证:
,求证:
(本小题满分12分)已知函数 ,
,
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若k为正常数,设 ,求函数
,求函数 的最小值;
的最小值;
(Ⅲ)若 ,证明:
,证明: .
.
已知中心在坐标原点,焦点在 轴上的椭圆过点
轴上的椭圆过点 ,且它的离心率
,且它的离心率 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)与圆 相切的直线
相切的直线 交椭圆于
交椭圆于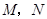 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数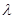 的取值范围.
的取值范围.
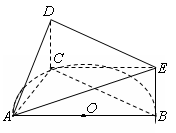
(本小题满分12分)如图, 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上除
上除 、
、 外的一个动点,
外的一个动点,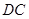 垂直于半圆
垂直于半圆 所在的平面,
所在的平面, 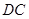 ∥
∥ ,
, ,
, ,
, .
.
(1)证明:平面 平面
平面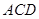 ;
;
(2)当三棱锥 体积最大时,求二面角
体积最大时,求二面角 的余弦值.
的余弦值.
某中学一名数学老师对全班 名学生某次考试成绩分男女生进行了统计(满分
名学生某次考试成绩分男女生进行了统计(满分 分),其中
分),其中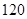 分(含
分(含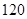 分)以上为优秀,绘制了如下的两个频率分布直方图:
分)以上为优秀,绘制了如下的两个频率分布直方图:
(Ⅰ)根据以上两个直方图完成下面的 列联表:
列联表: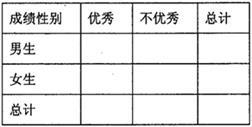
(Ⅱ)根据(Ⅰ)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(Ⅲ)若从成绩在 的学生中任取
的学生中任取 人,求取到的
人,求取到的 人中至少有
人中至少有 名女生的概率.
名女生的概率.