下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗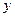 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
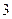 |
 |
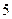 |
 |
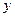 |
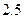 |
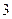 |
 |
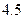 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出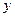 关于
关于 的线性回归方程
的线性回归方程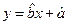 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性
回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
已知函数
在区间
,
内各有一个极值点.
(I)求
的最大值;
(II)当
时,设函数
在点
处的切线为
,若
在点
处穿过函数
的图象(即动点在点
附近沿曲线
运动,经过点
时,从
的一侧进入另一侧),求函数
的表达式.
设
是数列
(
)的前
项和,
,且
,
,
.
(I)证明:数列
是常数数列;
(II)试找出一个奇数
,使以18为首项,7为公比的等比数列
中的所有项都是数列
中的项,并指出
是数列
中的第几项.
已知双曲线
的右焦点为
,过点
的动直线与双曲线相交于
两点,点
的坐标是
.
(I)证明
,
为常数;
(II)若动点
满足
(其中
为坐标原点),求点
的轨迹方程.
如图,已知直二面角
,
,
,
,
,
,
和平面
所成的角为
.
(I)证明
;
(II)求二面角
的大小. 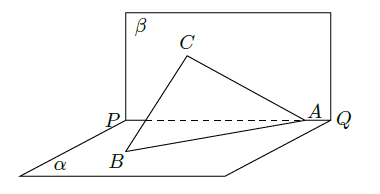
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有
,参加过计算机培训的有
,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,求这3人中至少有2人参加过培养的概率.