(13分)已知点A，B的坐标分别是（0，–1），（0，1），-优题课

题文

(13分) 已知点A，B的坐标分别是（0，–1），（0，1），直线AM，BM相交于点M，且它们的斜率之积为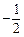．（10求点M的轨迹C的方程；(2)过D（2，0）的直线l与轨迹C有两不同的交点时，求l的斜率的取值范围；(3)若过点D（2，0）的直线l与(1)中的轨迹C交于不同的两点E、F（E在D、F之间），试求与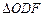面积之比的取值范围（O为坐标原点）；

科目数学题型解答题难度较易

登录免费查看答案和解析

相关试题

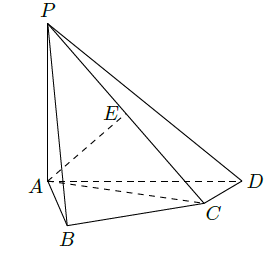
如图，在四棱锥 $P - A B C D$ 中， $P A ⊥$ 底面 $A B C D$ ， $A B ⊥ A D, A C ⊥ C D, ∠ A B C = 60^{°}, P A = A B = B C, E$ 是 $P C$ 的中点．
（Ⅰ）证明 $C D ⊥ A E$ ；
（Ⅱ）证明 $P D ⊥$ 平面 $A B E$ ；
（Ⅲ）求二面角 $A - P D - C$ 的大小．

已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑球．现从甲、乙两个盒内各任取2个球．
（Ⅰ）求取出的4个球均为黑球的概率；
（Ⅱ）求取出的4个球中恰有1个红球的概率；
（Ⅲ）设 $ξ$ 为取出的4个球中红球的个数，求 $ξ$ 的分布列和数学期望．

已知函数 $f (x) = 2 \cos x (\sin x - \cos x) + 1, x \in R$ ．
（Ⅰ）求函数 $f (x)$ 的最小正周期；
（Ⅱ）求函数 $f (x)$ 在区间 $[\frac{π}{8}, \frac{3 π}{4}]$ 上的最小值和最大值．

已知函数 $f (x) = \frac{1}{3} x^{3} + \frac{1}{2} a x^{2} + b x$ 在区间 $[- 1, 1)$ , $(1, 3]$ 内各有一个极值点．
（I）求 $a^{2} - 4 b$ 的最大值；
（II）当 $a^{2} - 4 b = 8$ 时，设函数 $y = f (x)$ 在点 $A (1, f (1))$ 处的切线为 $l$ ，若 $l$ 在点 $A$ 处穿过函数 $y = f (x)$ 的图象（即动点在点 $A$ 附近沿曲线 $y = f (x)$ 运动，经过点 $A$ 时，从 $l$ 的一侧进入另一侧），求函数 $y = f (x)$ 的表达式．

设 $S_{n}$ 是数列 $\{a_{n}\}$ （ $n \in N^{+}$ ）的前 $n$ 项和， $a_{1} = a$ ，且 $S n^{2} = 3 n^{2} a_{n} + {S_{n - 1}}^{2}$ ， $a_{n} \neq 0$ ， $n = 2, 3, 4, . . .$ ．
（I）证明：数列 $\{a_{n + 2} - a_{n}\}$ $(n \geq 2)$ 是常数数列；
（II）试找出一个奇数 $a$ ，使以18为首项，7为公比的等比数列 $\{b_{n}\} (n \in N^{*})$ 中的所有项都是数列 $\{a_{n}\}$ 中的项，并指出 $b_{n}$ 是数列 $\{a_{n}\}$ 中的第几项．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号