已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x–1)=f(3–x)且方程f(x)=2x有等根.
(1)求f(x)的解析式;
(2)是否存在实数m,n(m<n=,使f(x)定义域和值域分别为[m,n]和[4m,4n],如果存在,求出m、n的值;如果不存在,说明理由.
(本小题满分14分)计算下列各式的值:
(1)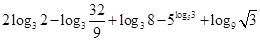 ;
;
(2)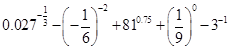 .
.
(本小题满分14分)设全集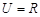 ,函数
,函数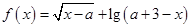 的定义域为集合
的定义域为集合 ,集合
,集合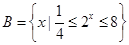 .
.
(1)若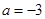 ,求
,求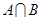 ,
,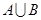 ;
;
(2)若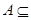 CUB,求实数
CUB,求实数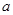 的取值范围.
的取值范围.
已知函数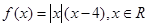 .
.
(1)将函数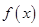 写成分段函数的形式,并作出函数的大致的简图(作图要求:①要求列表;②先用铅笔作出图象,再用
写成分段函数的形式,并作出函数的大致的简图(作图要求:①要求列表;②先用铅笔作出图象,再用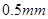 的黑色签字笔将图象描黑);
的黑色签字笔将图象描黑);
(2)根据函数的图象写出函数的单调区间,并写出函数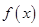 在区间
在区间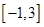 上的最大值和最小值.
上的最大值和最小值.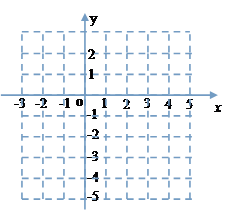
已知函数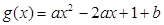 (
( )在区间
)在区间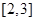 上有最大值
上有最大值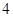 和最小值
和最小值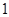 .设
.设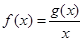 .
.
(1)求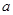 、
、 的值;
的值;
(2)若不等式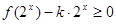 在
在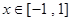 上恒成立,求实数
上恒成立,求实数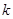 的取值范围;
的取值范围;
(3)若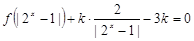 有三个不同的实数解,求实数
有三个不同的实数解,求实数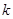 的取值范围.
的取值范围.
已知二次函数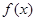 满足
满足 且
且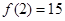 .
.
(1)求函数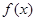 的解析式;
的解析式;
(2)令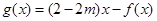
①若函数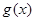 在
在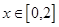 上是单调函数,求实数
上是单调函数,求实数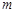 的取值范围;
的取值范围;
②求函数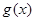 在
在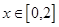 的最小值.
的最小值.