已知椭圆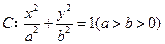 的左、右焦点分别是
的左、右焦点分别是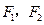 ,离心率为
,离心率为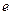 .直线
.直线 与
与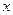 轴,
轴,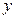 轴分别交于点
轴分别交于点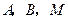 是直线
是直线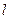 与椭圆
与椭圆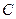 的一个公共点,
的一个公共点,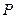 是点
是点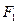 关于直线
关于直线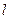 的对称点.设
的对称点.设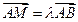 .
.
(Ⅰ)证明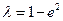 ;
;
(Ⅱ)若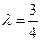 ,
,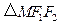 的周长为
的周长为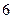 ,写出椭圆
,写出椭圆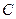 的方程;
的方程;
(Ⅲ)确定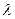 的值,使得
的值,使得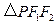 是等腰三角形.
是等腰三角形.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)若该校高一年级共有学生 人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(2)若从数学成绩在 与
与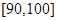 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。
在 中,
中,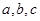 分别是角
分别是角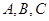 的对边,
的对边, ,
, .
.
(1)求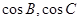 的值;
的值;
(2)若 ,求边
,求边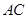 的长.
的长.
已知抛物线 (
(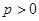 )上一点
)上一点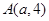 到其准线的距离为
到其准线的距离为 .
.
(Ⅰ)求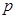 与
与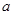 的值;
的值;
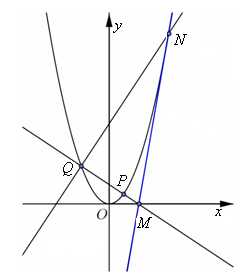
(Ⅱ)设抛物线 上动点
上动点 的横坐标为
的横坐标为 (
(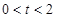 ),过点
),过点 的直线交
的直线交 于另一点
于另一点 ,交
,交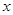 轴于
轴于 点(直线
点(直线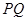 的斜率记作
的斜率记作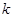 ).过点
).过点 作
作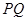 的垂线交
的垂线交 于另一点
于另一点 .若
.若 恰好是
恰好是 的切线,问
的切线,问 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
已知向量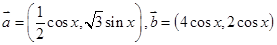 函数
函数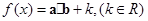
(Ⅰ)求 的单调增区间;
的单调增区间;
(Ⅱ)若 时,
时, 的最大值为4,求
的最大值为4,求 的值.
的值.
 A是锐角,求
A是锐角,求 的值;
的值;