已知锐角△ABC的三内角 所对的边分别为
所对的边分别为 ,边a、b是方程x2-2
,边a、b是方程x2-2 x+2=0的两根,角A、B满足关系2sin(A+B)-
x+2=0的两根,角A、B满足关系2sin(A+B)- =0,求角C的度数,边c的长度及△ABC的面积.
=0,求角C的度数,边c的长度及△ABC的面积.
某射击运动员为争取获得2010年广州亚运会的参赛资格正在加紧训练.已知在某次训练中他射击了 枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为
枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为 ,设
,设 为本次训练中成绩不低于10环的射击次数,
为本次训练中成绩不低于10环的射击次数, 的数学期望
的数学期望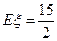 ,方差
,方差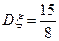 .
.
(1)求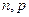 的值;
的值;
(2)训练中教练要求:若有5枪或5枪以上成绩低于10环,则需要补射,求该运动员在本次训练中需要补射的概率.
(结果用分数表示.已知: ,
,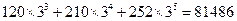 )
)
设向量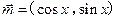 ,
,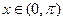 ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)设 ,求函数
,求函数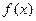 的值域.
的值域.
(1)若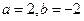 ,求函数
,求函数 的极值;
的极值;
(2)若 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出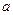 关于
关于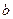 的关系式(用
的关系式(用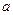 表示
表示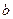 ),并确定
),并确定 的单调区间;
的单调区间;
(3)在(2)的条件下,设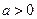 ,函数
,函数 .若存在
.若存在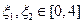 使得
使得 成立,求
成立,求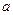 的取值范围.
的取值范围.
已知数列 和
和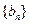 满足
满足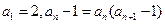 ,
, ,
, .
.
(1)求数列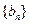 的通项公式;
的通项公式;
(2)设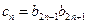 ,求使得
,求使得
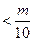 对一切
对一切 都成立的最小正整数
都成立的最小正整数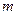 ;
;
(3)设数列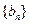 的前
的前 和为
和为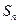 ,
,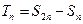 ,试比较
,试比较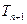 与
与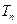 的大小.
的大小.
已知点C(1,0),点A、B是⊙O: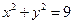 上任意两个不同的点,
上任意两个不同的点,
且满足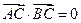 ,设P为弦AB的中点,
,设P为弦AB的中点,
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线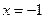 的
的
距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.