下表是某年美国旧轿车价格的调查资料，今以x表示轿车的使用年数,y表示相应的年均价格，求y关于x的回归
方程.
| 使用年数x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 年均价格 y（美元） |
2 651 |
1 943 |
1 494 |
1 087 |
765 |
538 |
484 |
290 |
226 |
204 |
（本小题满分16分）定义在R上的函数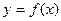
，
，当
时，
，且
对任意的
∈R，有
.
（1）求证：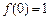
；
（2）求证：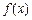
是R上的增函数；
（3）若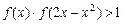
，求
的取值范围.
据气象中心观察和预测：发生于
地的沙尘暴一直向正南方向移动，其移动速度
与时间
的函数图象如图所示，过线段OC上一点
作横轴的垂线
，梯形
在直线左侧部分的面积即为内沙尘暴所经过的路程
.
（1）当
时，求
的值；
（2）将随
变化的规律用数学关系式表示出来；
（3）若
城位于地正南方向，且距地
，试判断这场沙尘暴是否会侵袭到城，如果会，在沙尘暴发生后多长时间它将侵袭到城？如果不会，请说明理由.
已知函数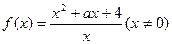
。
（Ⅰ）若
为奇函数，求
的值；
（Ⅱ）若在
上恒大于0，求的取值范围。
(本小题满分14分)
命题p：
且
;
命题q：集合
，
且
，
求实数
的取值范围,使命题p, q中至少有一个为真命题.
（本小题满分14分）
已知复数
满足
（1）求的值；（2）求
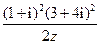的值。