已知a,b,c为互不相等的非负数.
求证:a2+b2+c2>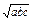 (
(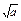 +
+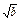 +
+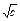 ).
).
四棱锥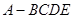 的侧面
的侧面 是等边三角形,
是等边三角形,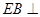 平面
平面 ,
,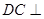 平面
平面 ,
,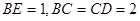 ,
,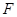 是棱
是棱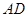 的中点.
的中点.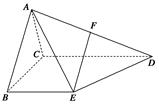
(1)求证: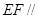 平面
平面 ;
;
(2)求四棱锥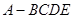 的体积.
的体积.
(本小题满分13分)已知椭圆 的中心在原点
的中心在原点 ,焦点
,焦点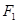 ,
,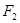 在
在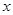 轴上,经过点
轴上,经过点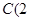 ,
, ,且抛物线
,且抛物线
 的焦点为
的焦点为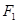 .
.
(1) 求椭圆 的方程;
的方程;
(2) 垂直于 的直线
的直线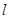 与椭圆
与椭圆 交于
交于 ,
,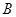 两点,当以
两点,当以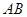 为直径的圆
为直径的圆 与
与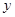 轴相切时,求直线
轴相切时,求直线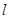 的方程和圆
的方程和圆 的方程.
的方程.
(本小题满分13分)某市“环保提案”对某处的环境状况进行了实地调研,据测定,该处的污染指数与附近污染源的强度成正比,与到污染源的距离成反比,比例常数为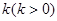 .现已知相距
.现已知相距 的
的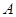 ,
, 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数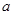 ,
,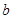 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数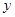 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设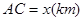 .
.
(1) 试将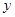 表示为
表示为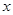 的函数;
的函数;
(2) 若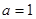 时,
时,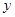 在
在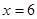 处取得最小值,试求
处取得最小值,试求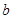 的值.
的值.
(本小题满分12分)已知数列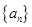 满足
满足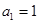 ,
,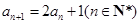 .
.
⑴求证:数列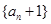 是等比数列,并写出数列
是等比数列,并写出数列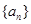 的通项公式;
的通项公式;
⑵若数列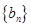 满足
满足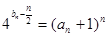 ,求
,求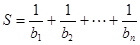 的值.
的值.
(本小题满分12分)已知锐角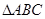 中内角
中内角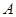 、
、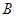 、
、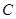 的对边分别为
的对边分别为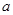 、
、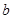 、
、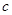 ,且
,且 .
.
(1)求角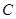 的值;
的值;
(2)设函数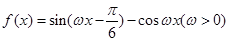 ,
,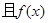 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为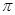 ,求
,求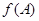 的取值范围.
的取值范围.