(1)已知扇形的周长为10,面积为4,求扇形中心角的弧度数;
(2)已知扇形的周长为40,当它的半径和中心角取何值时,才能使扇形的面积最大?最大面积是多少?
(本题16分) 设函数 ,且
,且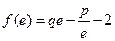 ,其中
,其中 是自然对数的底数.(1)求
是自然对数的底数.(1)求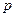 与
与 的关系;(2)若
的关系;(2)若 在其定义域内为单调函数,求
在其定义域内为单调函数,求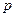 的取值范围;
的取值范围;
(3)设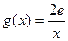 ,若在
,若在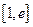 上至少存在一点
上至少存在一点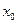 ,使得
,使得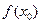 >
> 成立,求实数
成立,求实数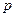 的取值范围.
的取值范围.
(本题16分)某国采用养老储备金制度,公民在就业的第一年就交纳养老储备金,数目为a1,以后每年交纳的数目均比上一年增加 d(d>0), 因此,历年所交纳的储备金数目a1, a2, … 是一个公差为 d的等差数列.与此同时,国家给予优惠的计息政府,不仅采用固定利率,而且计算复利. 这就是说,如果固定年利率为r(r>0),那么, 在第n年末,第一年所交纳的储备金就变为 a1(1+r)n-1,第二年所交纳的储备金就变成 a2(1+r)n-2,……. 以Tn表示到第n年末所累计的储备金总额.(Ⅰ)写出Tn与Tn-1(n≥2)的递推关系式;(Ⅱ)求证Tn=An+ Bn,其中{An}是一个等比数列,{Bn}是一个等差数列.
(本小题满分16分)已知F1(-c,0), F2(c,0) (c>0)是椭圆的两个焦点,O为坐标原点,圆M的方程是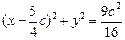 .
.
(1)若P是圆M上的任意一点,求证: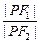 是定值;
是定值;
(2)若椭圆经过圆上一点Q,且cos∠F1QF2=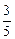 ,求椭圆的离心率;
,求椭圆的离心率;
(3)在(2)的条件下,若|OQ|=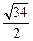 ,求椭圆的方程.
,求椭圆的方程.
(本题14分)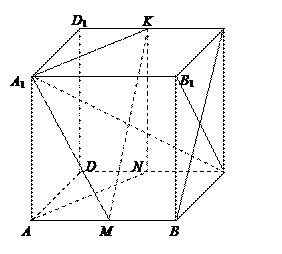 如图,
如图,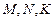 分别是正方体
分别是正方体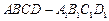 的
的
棱 的中点.
的中点.
(1)求证: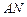 //平面
//平面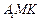 ;
;
(2)求证:平面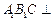 平面
平面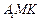 .
.
(本题14分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)
与相应的生产能耗y(吨标准煤)的几组对照数据
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程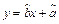 ;
;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤. 请进行线性相关性分析,如果有95﹪以上把握说具有线性相关性,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数据: 3×2.5+4×3+5×4+6×4.5=66.5)
| n-2 |
0.05 |
0.01 |
| 2 |
0.950 |
0.990 |