圆C过点P(1,2)和Q(-2,3),且圆C在两坐标轴上截得的弦长相等,求圆C的方程. 
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
| 患色盲 |
不患色盲 |
总计 |
|
| 男 |
442 |
||
| 女 |
6 |
||
| 总计 |
44 |
956 |
1000 |
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少?
随机变量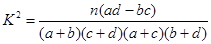
附临界值参考表:
| P(K2≥x0) |
0.10 |
0.05 |
0.025 |
0.10 |
0.005 |
0.001 |
| x0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知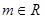 ,复数
,复数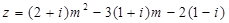 ,
,
(1)写出复数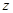 的代数形式;
的代数形式;
(2)当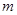 为何值时,
为何值时,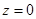 ?当
?当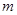 为何值时,
为何值时,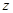 是纯虚数?
是纯虚数?
设函数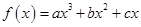 在区间
在区间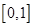 上是增函数,在区间
上是增函数,在区间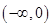 ,
,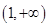 上是减函数,又
上是减函数,又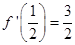
(1)求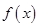 的解析式;
的解析式;
(2)若在区间
 上恒有
上恒有 成立,求
成立,求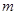 的取值范围
的取值范围
设数列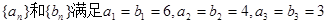 ,且数列
,且数列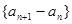 是等差数列,
是等差数列,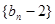 是等比数列.
是等比数列.
(1)求数列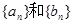 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为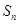 ,求
,求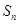 的表达式;
的表达式;
(3)数列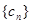 满足
满足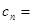
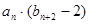 ,求数列
,求数列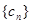 的最大项.
的最大项.
已知实数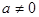 ,函数
,函数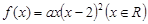 .
.
(Ⅰ)若函数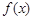 有极大值32,求实数
有极大值32,求实数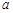 的值;
的值;
(Ⅱ)若对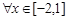 ,不等式
,不等式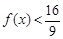 恒成立,求实数
恒成立,求实数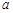 的取值范围.
的取值范围.