
已知椭圆 的对称点落在直线
的对称点落在直线 )上,且椭圆C的离心率为
)上,且椭圆C的离心率为
(1)求椭圆C的方程;
(2)设A(3,0),M、N是椭圆C上关于x轴对称的任意两点,连结AN交椭圆于另一点E,求证直线ME与x轴相交于定点.
(本小题满分12分)
△ABC的三个内角A,B,C所对的边分别为a,b,c,asinAsinB+bcos2A=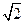 a.
a.
(I)求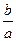 ;
;
(II)若c2=b2+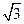 a2,求B.
a2,求B.
(本小题满分12分)
设函数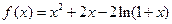 .
.
(1)求函数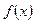 的单调区间;
的单调区间;
(2)当 时,是否存在整数
时,是否存在整数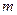 ,使不等式
,使不等式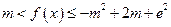 恒成立?若
恒成立?若
存在,求整数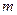 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3)关于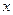 的方程
的方程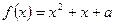 在
在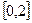 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数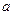 的取值范围。
的取值范围。
.(本小题满分12分)
已知数列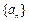 满足:
满足: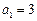 ,
,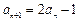 ,
,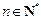 .计算得
.计算得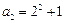 ,
,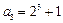 .
.
(1)猜想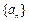 的通项公式
的通项公式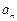 ,并用数学归纳法加以证明;
,并用数学归纳法加以证明;
(2)用反证法证明数列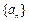 中不存在成等差数列的三项.
中不存在成等差数列的三项.
(本小题满分12分)
已知3名志愿者在10月1号至10月5号期间参加2011年国庆节志愿者活动工作.
(1)若每名志愿者在5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志原者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记 表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量 的数学期望.
的数学期望.
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为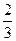 ,被乙小组攻克的概率为
,被乙小组攻克的概率为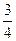 .
.
(1)设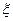 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求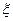 的分布列及
的分布列及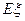 ;
;
(2)设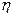 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件
在定义域内单调递增”为事件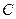 ,求事件
,求事件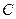 的概率.
的概率.