平面α内有5个点,平面β内有4个点,用其中4个点作一四面体的4个顶点,最多可构成多少个四面体?
已知等差数列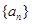 的前
的前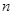 项和为
项和为 ,且
,且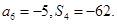
(1)求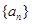 通项公式;
通项公式;
(2)求数列 的前
的前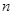 项和
项和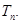
如图,某观测站C在城A的南偏西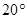 的方向,从城A出发有一条走向为南偏东
的方向,从城A出发有一条走向为南偏东 的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
甲、乙、丙三人在同一办公室工作,办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为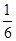 、
、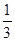 、
、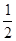 。若在同一时间内打进三个电话,且各个电话相互独立,求:
。若在同一时间内打进三个电话,且各个电话相互独立,求: 这三个电话是打给同一个人的概率;
这三个电话是打给同一个人的概率; 这三个电话中恰有两个是打给甲的概率。
这三个电话中恰有两个是打给甲的概率。
已知函数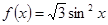
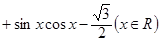 。
。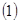 若
若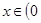 ,
,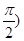 ,求
,求 的最大值;
的最大值;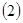 在
在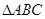 中,若
中,若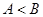 ,
, ,求
,求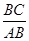 的值。
的值。
已知三次函数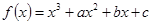 在
在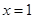 和
和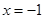 时取极值,且
时取极值,且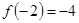 。
。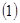 求函数
求函数 的表达式;
的表达式;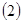 求函数
求函数 的单调区间和极值;
的单调区间和极值;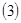 若函数
若函数
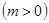 在区间
在区间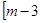 ,
,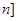 上的值域为
上的值域为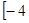 ,16
,16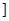 ,试求
,试求 、
、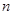 应满足的条件。
应满足的条件。