已知 函数f(x)=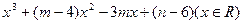
的图像关于原点对称，其中m,n为实常数。
（１）求m , n的值；
（２）试用单调性的定义证明：f (x) 在区间[-2, 2] 上是单调函数；
（３）[理科做] 当-2≤x≤2 时，不等式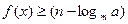
恒成立，求实数a的取值范围。
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定（平面图如图所示），如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/米2，水池所有墙的厚度忽略不计.
（1）试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；
（2）若由于地形限制，该池的长和宽都不能超过16米，试设计污水池的长和宽，使总造价最低.
在三棱锥
中，
和
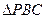是边长为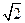
的等边三角形，
，
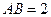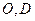分别是
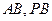的中点．
（1）求证：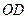
∥平面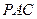
；
（2）求证：平面
⊥平面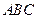
；
（3）求三棱锥的体积．
已知圆心在x轴正半轴的圆C经过A（2,0），且与双曲线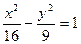
的渐近线相切，
求圆C的方程
设函数
（1）求
的单调递增区间；
（2）当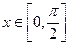
时，求的值域。
定义：若对定义域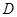
内的任意两个
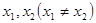，均有
成立，则称函数
是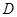上的“平缓函数”。
1.判断
和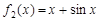
的单调性并证明；
2.判断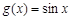
和
是否为R上的“平缓函数”,并说明理由；
3.若数列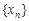
中，
总有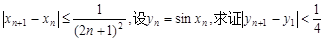
。