已知双曲线G的中心在原点,它的渐近线与圆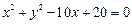 相切,过点P(-4,0)作斜率为
相切,过点P(-4,0)作斜率为 的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足
的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足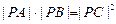
(1)求双曲线G的渐近线方程
(2)求双曲线G的方程
(3)椭圆S的中心在原点,它的短轴是G的实轴,如果S中垂直于l的平行弦的中点轨迹恰好是G的渐近线截在S内的部分,求椭圆S的方程。
已知
是公差不为零的等差数列,
,且
成等比数列.
(Ⅰ)求数列
的通项;
(Ⅱ)求数列 的前 项和 .
已知抛物线
的焦点为
,过点
的直线
与
相交于
、
两点,点
关于
轴的对称点为
.
(Ⅰ)证明:点
在直线
上;
(Ⅱ)设
,求
的内切圆
的方程 .
已知函数
.
(Ⅰ)当
时,求
的极值;
(Ⅱ)若
在
上是增函数,求
的取值范围.
如图,四棱锥 中, 底面 , , , , , 为棱 上的一点,平面 平面 .
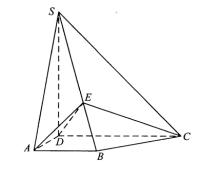
(Ⅰ)证明:
;
(Ⅱ)求二面角
的大小.
投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3.各专家独立评审.
(I)求投到该杂志的1篇稿件被录用的概率;
(II)求投到该杂志的4篇稿件中,至少有2篇被录用的概率.