设全集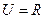 ,集合
,集合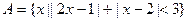 ,
,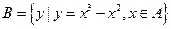 ,求
,求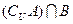
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: (a>0),过点P(-2,-4)的直线l的参数方程为
(a>0),过点P(-2,-4)的直线l的参数方程为 (t为参数),l与C分别交于M,N.
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.
(1)求证:AT2=BT·AD;
(2)E、F是BC的三等分点,且DE=DF,求∠A.
椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,P(m,0)为C的长轴上的一个动点,过P点斜率为
,P(m,0)为C的长轴上的一个动点,过P点斜率为 的直线l交C于A、B两点.当m=0时,
的直线l交C于A、B两点.当m=0时,
(1)求C的方程;
(2)求证: 为定值.
为定值.
已知函数f(x)=2ex-ax-2(a∈R)
(1)讨论函数的单调性;
(2)当x≥0时,f(x)≥0,求a的取值范围.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点.
(1)求证:A1B∥平面ADC1;
(2)若AB=AC,BC=AA1=2,求点A1到平面ADC1的距离.