(本小题满分16分)已知圆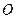 :
: 交
交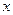 轴于
轴于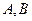 两点,曲线
两点,曲线 是以
是以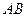 为长轴,直线:
为长轴,直线: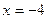 为准线的椭圆.(1)求椭圆的标准方程;(2)若
为准线的椭圆.(1)求椭圆的标准方程;(2)若 是直线上的任意一点,以
是直线上的任意一点,以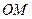 为直径的圆
为直径的圆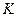 与圆
与圆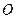 相交于
相交于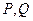 两点,求证:直线
两点,求证:直线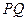 必过定点
必过定点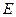 ,并求出点
,并求出点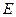 的坐标;(3)如图所示,若直线
的坐标;(3)如图所示,若直线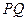 与椭圆
与椭圆 交于
交于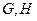 两点,且
两点,且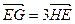 ,试求此时弦
,试求此时弦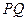 的长.
的长.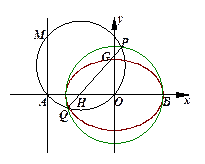
 ABC中内角A,B,C的对边分别为a,b,c,已知2a=
ABC中内角A,B,C的对边分别为a,b,c,已知2a=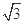 c,
c, .
.
(I)求 的值;
的值;
(II)若D为AC中点,且 ABD的面积为
ABD的面积为 ,求BD长。
,求BD长。
已知函数 .
.
(1)求函数 的单调区间; (2)若
的单调区间; (2)若 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)证明: 
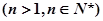
已知函数f(x)=ax3+bx2-x(x∈R,a、b是常数,a≠0),且当x=1和x=2时,函数f(x)取得极值.(I)求函数f(x)的解析式;
(Ⅱ)若曲线y=f(x)与g(x)=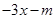
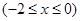 有两个不同的交点,求实数m的取值范围.
有两个不同的交点,求实数m的取值范围.
已知m∈R,对p:x1和x2是方程x2-ax-2=0的两个根,不等式|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立;q:函数f(x)=3x2+2mx+m+ 有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
提高过江大桥的车辆通行能力可改善整个城市的交通状况。在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当 时,车流速度
时,车流速度 是车流密度
是车流密度 的一次函数。
的一次函数。
当 时,求函数
时,求函数 的表达式;
的表达式;
当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时)