已知向量 (
(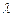 cos
cos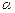 ,
,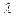 sin
sin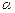 ) (
) (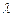 ≠0 ),
≠0 ),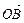 =" (" – sin
=" (" – sin ,cos
,cos ),其中O为坐标原点。(1)若
),其中O为坐标原点。(1)若 =
=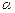 –
–  ,求向量
,求向量 与
与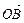 的夹角;(2)若|
的夹角;(2)若| |≥2|
|≥2|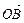 |对任意实数
|对任意实数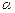 、
、 都成立,求实数
都成立,求实数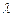 的取值范围。
的取值范围。
已知 为等差数列, 为等比数列, .
(Ⅰ)求 和 的通项公式;
(Ⅱ)记 的前 项和为 ,求证: ;
(Ⅲ)对任意的正整数 ,设 求数列 的前 项和.
已知椭圆 的一个顶点为 ,右焦点为 ,且 ,其中 为原点.
(Ⅰ)求椭圆 方程;
方程;
(Ⅱ)已知点 满足 ,点 在椭圆上( 异于椭圆的顶点),直线 与以 为圆心的圆相切于点 ,且 为线段 的中点.求直线 的方程.
如图,在三棱柱 中, 平面 , ,点 分别在棱 和棱 上,且 为棱 的中点.

(Ⅰ)求证: ;
(Ⅱ)求二面角 的正弦值;
(Ⅲ)求直线 与平面 所成角的正弦值.
在
中,角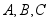 所对的边分别为
.已知
.
所对的边分别为
.已知
.
(Ⅰ)求角 的大小;
(Ⅱ)求 的值;
(Ⅲ)求 的值.
已知 ,函数 ,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数 在
上有唯一零点;
在
上有唯一零点;
(Ⅱ)记x0为函数 在
上的零点,证明:
在
上的零点,证明:
(ⅰ) ;
(ⅱ) .