(本小题满分12分)
在数列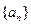 中,
中, .
.
(1)求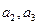 的值;
的值;
(2)求数列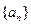 的通项公式;
的通项公式;
(3)求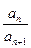 的最大值.
的最大值.
设全集为 ,集合
,集合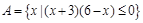 ,
, .
.
(1)求如图阴影部分表示的集合;
(2)已知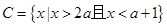 ,若
,若 ,求实数
,求实数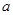 的取值范围.
的取值范围.
已知直线l经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0 .
(1)求直线l的方程;(2)求直线l关于原点O对称的直线方程。
在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.
(1)求此次参加竞赛的学生总数共有多少人?
(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?
若一批白炽灯共有10000只,其光通量X服从正态分布,其正态分布密度函数是f(x)= ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
(1)(203,215);(2)(191,227).
已知某种零件的尺寸X(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,且f(80)= .
.
(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.