(本小题满分12分)
已知函数
(1)确定 上的单调性;
上的单调性;
(2)设 在(0,2)上有极值,求
在(0,2)上有极值,求 的取值范围。
的取值范围。
(本小题满分12分)
在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格。
(1)用样本估计总体,请根据茎叶图对甲乙两个班级的成绩进行比较。
(2)求从甲班10名学生和乙班10名学生中各抽取一人,已知有人及格的条件下乙班同学不及格的概率;
(3)从甲班10人中抽取一人,乙班10人中抽取二人,三人中及格人数记为X,求X的分布列和期望。
(本小题满分12分)已知函数 .
.
(Ⅰ)求函数 的最大值,并写出
的最大值,并写出 取最大值时
取最大值时 的取值集合;
的取值集合;
(Ⅱ)已知 中,角A,B,C的对边分别为a,b,c若
中,角A,B,C的对边分别为a,b,c若 b+c=2。求实数a的取值范围。
b+c=2。求实数a的取值范围。
已知无穷数列 的各项均为正整数,
的各项均为正整数, 为数列
为数列 的前
的前 项和.
项和.
(Ⅰ)若数列 是等差数列,且对任意正整数
是等差数列,且对任意正整数 都有
都有 成立,求数列
成立,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数 ,从集合
,从集合 中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与
中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与 一起恰好是1至
一起恰好是1至 全体正整数组成的集合.
全体正整数组成的集合.
(ⅰ)求 的值;(ⅱ)求数列
的值;(ⅱ)求数列 的通项公式.
的通项公式.
已知函数 ,其中
,其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若 在
在 上存在最大值和最小值,求
上存在最大值和最小值,求 的取值范围.
的取值范围.
若椭圆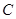 的方程为
的方程为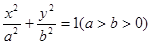 ,
, 、
、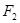 是它的左、右焦点,椭圆
是它的左、右焦点,椭圆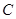 过点
过点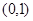 ,且离心率为
,且离心率为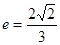 .
.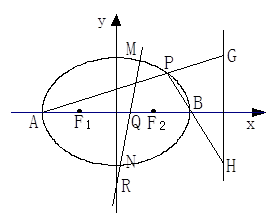
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左右顶点为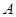 、
、 ,直线
,直线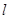 的方程为
的方程为 ,
,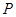 是椭圆上任一点,直线
是椭圆上任一点,直线 、
、 分别交直线
分别交直线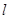 于
于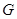 、
、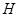 两点,求
两点,求 的值;
的值;
(Ⅲ)过点 任意作直线
任意作直线 (与
(与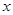 轴不垂直)与椭圆
轴不垂直)与椭圆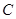 交于
交于 、
、 两点,与
两点,与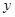 轴交于
轴交于 点
点 ,
, .证明:
.证明: 为定值.
为定值.