已知 ,
(Ⅰ)求
的值;
(Ⅱ)求
的值.
已知 ,
, , 且
, 且 .
.
(1)求函数 的解析式;
的解析式;
(2)当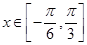 时,
时,  的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数 的最大值, 并求出相应的
的最大值, 并求出相应的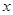 的值.
的值.
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(Ⅰ)从中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
已知 ,
, ,当
,当 为何值时,
为何值时,
(1)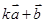 与
与 垂直?(2)
垂直?(2)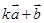 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
在平面直角坐标系中,O为坐标原点,已知向量 ,又点
,又点 ,
,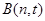 ,
,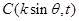 .
.
(1)若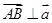 ,且
,且 ,求向量
,求向量 .
.
(2)若向量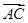 与向量
与向量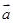 共线,常数
共线,常数 ,当
,当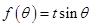 取最大值4时,求
取最大值4时,求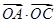 .
.