用等值法求161,253的最大公约数.
袋中有同样的球5个,其中3个红色,2个黄色,现从中随机且不返回地摸球,每次摸1个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:
为此时已摸球的次数,求:
(1)随机变量 的概率分布列;(2)随机变量
的概率分布列;(2)随机变量 的数学期望与方差.
的数学期望与方差.
有六节电池,其中有2只没电,4只有电,每次随机抽取一个测试,不放回,直至分清楚有电没电为止,所要测试的次数 为随机变量,求
为随机变量,求 的分布列.
的分布列.
在10件产品中有2件次品,连续抽3次,每次抽1件,求:
(1)不放回抽样时,抽到次品数 的分布列;
的分布列;
(2)放回抽样时,抽到次品数 的分布列.
的分布列.
如图,已知平行六面体 的底面ABCD是菱形,且
的底面ABCD是菱形,且 ,(1)证明:
,(1)证明: ;
;
(II)假定CD=2, ,记面
,记面 为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
(III)当 的值为多少时,能使
的值为多少时,能使 ?请给出证明.
?请给出证明.
已知 的顶点分别为
的顶点分别为 ,
, 在直线
在直线 上.
上.
(Ⅰ)若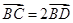 ,求点
,求点 的坐标;
的坐标;
(Ⅱ)若 ,求点
,求点 的坐标.
的坐标.