已知数列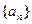 满足
满足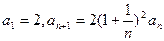
(1) 求数列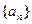 的通项公式;
的通项公式;
(2) 设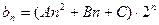 ,试推断是否存在常数A、B、C,使对一切
,试推断是否存在常数A、B、C,使对一切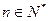 都有
都有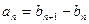 成立?若存在,求出A、B、C的值;若不存在,说明理由;
成立?若存在,求出A、B、C的值;若不存在,说明理由;
(3)求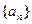 的前n项和
的前n项和
(本题12分)若函数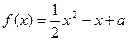 的定义域和值域均为[1,b](b>1),求a,b的值.
的定义域和值域均为[1,b](b>1),求a,b的值.
(本题12分)已知函数f (x)=x 2+ax ,且对任意的实数x都有f (1+x)=f (1-x) 成立.
(1)求实数 a的值;
(2)利用单调性的定义证明函数f(x)在区间[1,+∞ 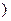 上是增函数.
上是增函数.
(本题12分)(1)已知f (x+1)=x2+4x+1,求f (x)的解析式;
(2)已知f (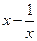 )=
)=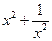 +1,求f (x) 的解析式.(不必写出定义域)
+1,求f (x) 的解析式.(不必写出定义域)
(本题10分)已知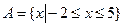 ,
,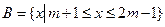 ,
,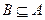 ,求
,求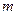 的取值范围。
的取值范围。
(本大题满分13分)设函数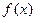 是定义域在
是定义域在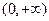 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数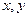 有
有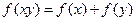 ,已知
,已知 .
.
(1)求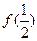 的值;
的值;
(2)一个各项均为正数的数列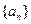 满足:
满足: ,其中
,其中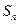 是数列
是数列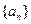 的前n项的和,求数列
的前n项的和,求数列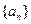 的通项公式;
的通项公式;
(3)在(2)的条件下,是否存在正数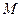 ,使
,使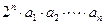


 对一切
对一切 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.