正定中学组织东西两校学生,利用周日时间去希望小学参加献爱
心活动,东西两校均至少有1名同学参加。已知东校区的每位同学往返车费是3元,
每人可为5名小学生服务;西校区的每位同学往返车费是5元,每人可为3位小学
生服务。如果要求西校区参加活动的同学比东校区的同学至少多1人,且两校区同
学去希望小学的往返总车费不超过37元。怎样安排东西两校参与活动同学的人数,
才能使受到服务的小学生最多?受到服务的小学生最多是多少?
(本小题共16 分)
分)
已知数列 各项均不为0,其前
各项均不为0,其前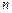 项和为
项和为 ,且对任意
,且对任意 都有
都有 (
(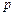 为大于1的常数),记f(n)
为大于1的常数),记f(n) .
.
(1)求 ;
;
(2)试比较 与
与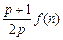 的大小(
的大小( );
);
(3)求证:(2n-1)f(n)≤f(1)+f(2)+…+f(2n-1) ≤[1-()2n-1] (n∈N*)
(本小题共16分)
已 知M(p, q)为直线x+y-m=0与曲线y=-的交点,且p<q,若f(x)=,λ、μ为正实数。求证:|f()-f()|<|p-q|
知M(p, q)为直线x+y-m=0与曲线y=-的交点,且p<q,若f(x)=,λ、μ为正实数。求证:|f()-f()|<|p-q|
(本小题共16分)
已知椭圆 和圆
和圆 :
: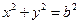 ,过椭圆上一点
,过椭圆上一点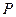 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为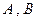 .
.
(1)①若圆 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率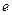 ; ②若椭圆上存在点
; ②若椭圆上存在点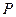 ,使得
,使得 ,求椭圆离心率
,求椭圆离心率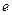 的取值范围;
的取值范围;
(2)设直线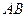 与
与 轴、
轴、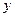 轴分别交于点
轴分别交于点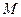 ,
, ,求证:
,求证: 为定值.
为定值.
((本小题满分14分)
如图:设工地有一个吊臂长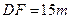 的吊车,吊车底座
的吊车,吊车底座 高
高 ,现准备把一个底半径为
,现准备把一个底半径为 高
高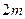 的圆柱形工件吊起平放到
的圆柱形工件吊起平放到 高的桥墩上,问能否将工件吊到桥墩上?(参考数据:
高的桥墩上,问能否将工件吊到桥墩上?(参考数据: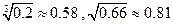 )
)
(本小题满分14分)
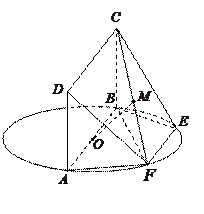
如图,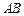 为圆
为圆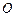 的直径,点
的直径,点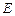 、
、 在圆
在圆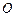 上,且
上,且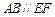 ,矩形
,矩形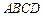 所在的平面和圆
所在的平面和圆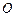 所在的平面互相垂直,且
所在的平面互相垂直,且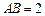 ,
,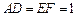 .
.
(1)求证: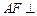 平面
平面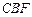 ;
;
(2)设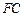 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
; (3)设平面
(3)设平面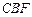 将几何体
将几何体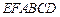 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
,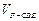 ,
,
求