(本小题共12)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
对于函数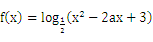 ,解答下列问题:
,解答下列问题:
(1)若 定义域为R,求实数a的取值范围;
定义域为R,求实数a的取值范围;
(2)若函数 在
在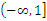 内为增函数,求实数a的取值范围.
内为增函数,求实数a的取值范围.
已知函数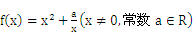
(1)判断函数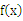 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2) 若函数数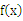 在区间
在区间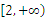 上是增函数,求实数a的取值范围。
上是增函数,求实数a的取值范围。
设函数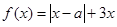 ,其中
,其中 。
。
(Ⅰ)当 时,求不等式
时,求不等式 的解集
的解集
(Ⅱ)若不等式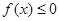 的解集为
的解集为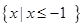 ,求a的值。
,求a的值。
在直角坐标系xOy中,曲线C1的参数方程为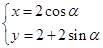 (
(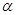 为参数)M是C1上的动点,P点满足
为参数)M是C1上的动点,P点满足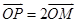 ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2
(Ⅰ)求C2的方程
(Ⅱ)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求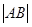 .
.
如图,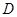 ,
,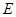 分别为
分别为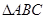 的边
的边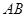 ,
, 上的点,且不与
上的点,且不与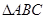 的顶点重合。已知
的顶点重合。已知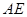 的长为
的长为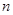 ,
, ,
,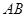 的长是关于
的长是关于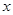 的方程x2-14x+mn=0的两个根。
的方程x2-14x+mn=0的两个根。
(Ⅰ)证明: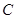 ,
,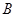 ,
,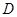 ,
,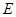 四点共圆;
四点共圆;
(Ⅱ)若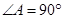 ,且
,且 ,求
,求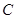 ,
,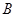 ,
,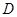 ,
,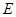 所在圆的半径。
所在圆的半径。