如图,四棱锥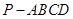 中,
中,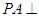 面
面 ,
,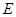 、
、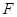 分别为
分别为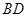 、
、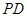 的中点,
的中点,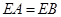 .
.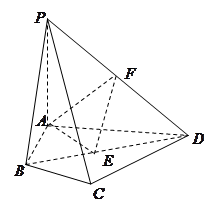
(1)证明: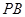 ∥面
∥面 ;
;
(2)证明: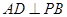
(本小题15分)已知△ABC三个顶点的坐标分别是A(0,2),B(1,1),C(1,3).若△ABC在一个切变变换T作用下变为△A1B1C1,其中B(1,1)在变换T作用下变为点B1(1,-1).
(1)求切变变换T所对应的矩阵M;
(2)将△A1B1C1绕原点按顺时针方向旋转45°后得到△A2B2C2.求B1变化后的对应点B2的坐标.
(本小题14分)在平面直角坐标系中,曲线C1的参数方程为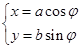 (a>b>0,
(a>b>0, 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点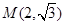 对应的参数
对应的参数 .
.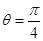 与曲线C2交于点
与曲线C2交于点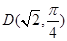 .
.
(1)求曲线C1,C2的直角坐标方程;
(2)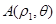 ,
, 是曲线C1上的两点,求
是曲线C1上的两点,求 的值.
的值.
(本小题14分)在极坐标系中,已知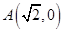 到直线l:
到直线l: 的距离为3.
的距离为3.
(1)求m的值.
(2)设P是直线l上的动点,点Q在线段OP上,满足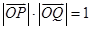 ,求点Q的轨迹方程.
,求点Q的轨迹方程.
如图,已知抛物线 的顶点D的坐标为(1,
的顶点D的坐标为(1, ),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
(l)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围;
(3)当P点的横坐标 时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF= (AD+BC)
(AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点
请你运用所学知识,结合上述材料,解答下列问题.
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD= ,OC=5,求MN的长.
,OC=5,求MN的长.