已知直线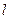 的参数方程为
的参数方程为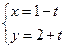 ,曲线
,曲线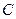 的极坐标方程为
的极坐标方程为 .
.
(1)将直线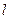 的参数方程化为普通方程;以极点为直角坐标系的原点,极轴为
的参数方程化为普通方程;以极点为直角坐标系的原点,极轴为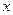 轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线
轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线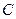 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若 为直线
为直线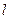 上任一点,
上任一点,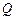 是曲线
是曲线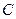 上任一点,求
上任一点,求 的最小值.
的最小值.
如右图,在棱长为a的正方体ABCDA1B1C1D1中,G为△BC1D的重心,
(1)试证:A1、G、C三点共线;
(2)试证:A1C⊥平面BC1D;
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=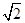 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.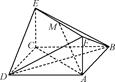
求证:(1)AM∥平面BDE;
(2)AM⊥平面BDF.
已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4).设a= ,b=
,b=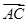 .
.
(1)求a和b的夹角θ;
(2)若向量ka+b与ka-2b互相垂直,求k的值.
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…,(-1) ,即当
,即当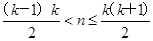 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
设函数f(x)=x-xlnx,数列{an}满足0<a1<1,an+1=f(an).求证:
(1)函数f(x)在区间(0,1)是增函数;
(2)an<an+1<1.