(理)已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (
( 为参数),直线
为参数),直线 与曲线C相交于
与曲线C相交于 两点,又点
两点,又点 的坐标为
的坐标为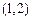 .
.
求:(1)线段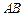 的中点坐标;
的中点坐标;
(2)线段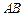 的长;
的长;
(3) 的值.
的值.
(文)已知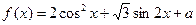 (
( ,
,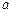 为常数).
为常数).
(1)若 ,求
,求 的最小正周期;
的最小正周期;
(2)若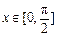 时,
时, 的最大值为4,求
的最大值为4,求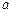 的值.
的值.
(本小题满分12分)营养学家指出,高中学生良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪.1kg食物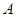 含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费
含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费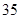 元;而1kg食物
元;而1kg食物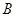 含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费
含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费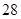 元.为了满足营养专家指出的 日常饮食要求,同时使花费最低,需要同时食用食物
元.为了满足营养专家指出的 日常饮食要求,同时使花费最低,需要同时食用食物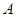 和食物
和食物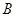 多少kg?
多少kg?
(本小题满分12分)已知函数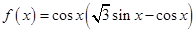 .
.
(1)求函数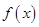 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)记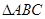 的内角
的内角 的对应边分别为
的对应边分别为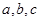 ,且
,且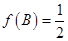 ,
,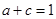 ,求
,求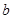 的取值范围.
的取值范围.
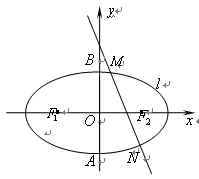
如图所示,椭圆C: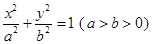 的两个焦点为
的两个焦点为 、
、 ,短轴两个端点为
,短轴两个端点为 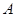 、
、 .已知
.已知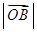 、
、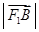 、
、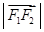 成等比数列,
成等比数列,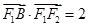 ,与
,与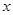 轴不垂直的直线
轴不垂直的直线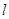 与 C 交于不同的两点
与 C 交于不同的两点 、
、 ,记直线
,记直线 、
、 的斜率分别为
的斜率分别为 、
、 ,且
,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求证直线 与
与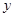 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标;
(Ⅲ)当弦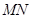 的中点
的中点 落在四边形
落在四边形 内(包括边界)时,求直线
内(包括边界)时,求直线 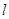 的斜率的取值范围.
的斜率的取值范围.
已知数列{ }中,
}中, ,且
,且 对任意正整数都成立,数列{
对任意正整数都成立,数列{ }的前n项和为
}的前n项和为
(1)若 ,且
,且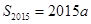 ,求a;
,求a;
(2)是否存在实数k,使数列{ }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项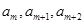 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若 .
.
(原创)已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得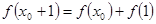 成立.
成立.
(1)函数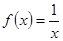 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(2)设函数 ,求
,求 的取值范围;
的取值范围;
(3)设函数 图象与函数
图象与函数 的图象有交点,证明:函数
的图象有交点,证明:函数 .
.