(本小题满分12分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
乙厂 乙厂
乙厂
(1)、试分别估计两个分厂生产的零件的优质品率;
(2)、由以上统计数据填下面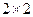 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| |
甲 厂 |
乙 厂 |
合计 |
| 优质品 |
|
|
|
| 非优质品 |
|
|
|
| 合计 |
|
|
|
附: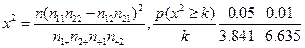
已知函数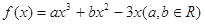 ,在点
,在点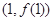 处的切线方程为
处的切线方程为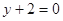 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有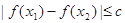 ,求实数
,求实数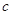 的最小值;
的最小值;
(Ⅲ)若过点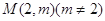 ,可作曲线
,可作曲线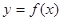 的三条切线,求实数
的三条切线,求实数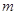 的取值范围.
的取值范围.
已知椭圆C: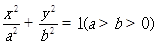 的离心率为
的离心率为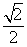 ,其中左焦点
,其中左焦点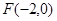 .
.
(Ⅰ)求出椭圆C的方程;
(Ⅱ) 若直线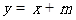 与曲线C交于不同的A、B两点,且线段AB的中点M在圆
与曲线C交于不同的A、B两点,且线段AB的中点M在圆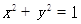 上,求m的值.
上,求m的值.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,
且AC=AD=CD=DE=2,AB=1.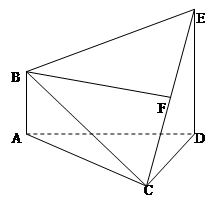
(Ⅰ)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(Ⅱ)求多面体ABCDE的体积.
已知函数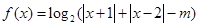 .
.
(Ⅰ)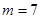 时,求函数
时,求函数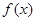 的定义域;
的定义域;
(Ⅱ)若关于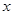 的不等式
的不等式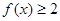 的解集是R,求
的解集是R,求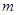 的取值范围.
的取值范围.
在△ABC中,角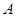 、
、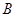 、
、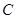 所对的边分别为
所对的边分别为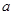 、
、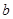 、
、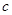 ,已知向量
,已知向量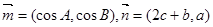 ,且
,且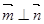 .
.
(Ⅰ) 求角A的大小;
(Ⅱ) 若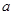
 ,
,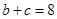 ,求△ABC的面积.
,求△ABC的面积.