(本题满分12分)
已知锐角△ABC中,角A、B、C的对边分别为 ,
,
且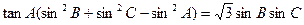 .
.
(1)求角A;
(2)求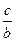 的范围.
的范围.
设椭圆的中心是坐标原点,焦点在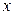 轴上,离心率
轴上,离心率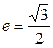 ,已知点
,已知点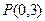 到这个椭圆上的点的最远距离是4,求这个椭圆的方程.
到这个椭圆上的点的最远距离是4,求这个椭圆的方程.
在平面直角坐标系中,若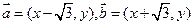 ,且
,且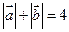 ,
,
(1)求动点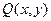 的轨迹
的轨迹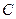 的方程;
的方程;
(2)已知定点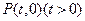 ,若斜率为
,若斜率为 的直线
的直线 过点
过点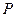 并与轨迹
并与轨迹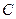 交于不同的两点
交于不同的两点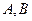 ,且对于轨迹
,且对于轨迹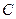 上任意一点
上任意一点 ,都存在
,都存在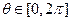 ,使得
,使得 成立,试求出满足条件的实数
成立,试求出满足条件的实数 的值。
的值。
若F 、F
、F 为双曲线
为双曲线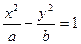 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足;
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足;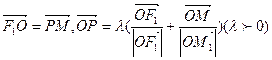 .
.
(1)求该双曲线的离心率;
(2)若该双曲线过N(2,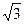 ),求双曲线的方程;
),求双曲线的方程;
(3)若过N(2,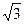 )的双曲线的虚轴端点分别为B
)的双曲线的虚轴端点分别为B 、B
、B (B
(B 在y轴正半轴上),点A、B在双曲线上,且
在y轴正半轴上),点A、B在双曲线上,且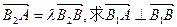 时,直线AB的方程.
时,直线AB的方程.
已知椭圆 的一条准线方程是
的一条准线方程是 其左、右顶点分别是A、B;双曲线
其左、右顶点分别是A、B;双曲线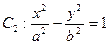 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0.
(Ⅰ)求椭圆C1的方程及双曲线C2的离心率;
(Ⅱ)在第一象限内取双曲线C2上一点P,连结AP交椭圆C1于点M,连结PB并延长交椭圆C1于点N,若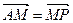 . 求证:
. 求证: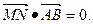
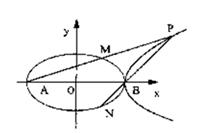
如图,直线l1与l2是同一平面内两条互相垂直的直线,交点是A,点B、D在直线l1上(B、D 位于点A右侧),且|AB|=4,|AD|=1,M是该平面上的一个动点,M在l1上的射影点是N,且|BN|=2|DM|.
(Ⅰ) 建立适当的坐标系,求动点M的轨迹C的方程.
(Ⅱ)过点D且不与l1、l2垂直的直线l交(Ⅰ)中的轨迹C于E、F两点;另外平面上的点G、H满足:①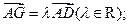 ②
②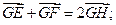 ③
③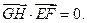 求点G的横坐标的取值范围.
求点G的横坐标的取值范围.