（本小题满分14分）
如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的
倍，P为侧棱SD上的点。
（1）求证：AC⊥SD；
（2）若SD⊥平面PAC，求二面角P-AC-D的大小；
（3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC。若存在，求SE：EC的值；若不存在，试说明理由。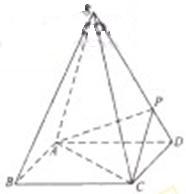
如图，在四棱锥A—BCDE中，底面BCDE为矩形，AB=AC，BC=2，CD=1，并且侧面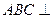
底面BCDE。
（1）取CD的中点为F，AE的中点为G，证明：FG//面ABC；
（2）试在线段BC上确定点M，使得AE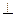
DM，并加以证明。
(本小题满分12分)已知函数
满足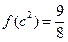
．
（1）求常数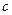
的值；（2）解不等式
．
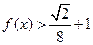(本小题满分12分)已知向量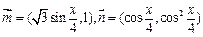
.
（1）若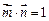
,求
的值；
（2）记
，在△ABC中，角
的对边分别是
且满足
，求函数f(A)的取值范围.
（本小题满分13分）
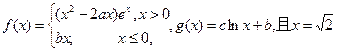已知函数
是函数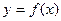
的极值点。
（I）求实数a的值，并确定实数m的取值范围，使得函数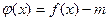
有两个零点；
（II）是否存在这样的直线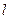
，同时满足：①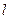是函数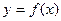的图象在点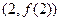
处的切线②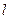与函数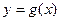
的图象相切于点
，如果存在，求实数b的取值范围；不存在，请说明理由。
（本小题满分13分）
已知椭圆C：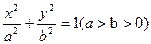
的左、右顶点的坐标分别为
,
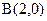，离心率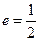
。
（Ⅰ）求椭圆C的方程：
（Ⅱ）设椭圆的两焦点分别为
,
，点P是其上的动点，
（1）当 
内切圆的面积最大时，求内切圆圆心的坐标；
（2）若直线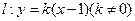
与椭圆交于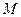
、
两点，证明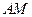直线
与直线
的交点在直线
上。