(本题满分12分)本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知直线l: 与双曲线C:
与双曲线C: 相交于A、B两点.
相交于A、B两点.
(1)求实数a的取值范围;
(2)当实数a取何值时,以线段AB为直径的圆经过坐标原点.
给定锐角三角形PBC,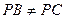 .设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
.设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
(1)若A,B,C,D四点共圆,求证: ;
;
(2)若 ,是否一定有A,B,C,D四点共圆?证明你的结论.
,是否一定有A,B,C,D四点共圆?证明你的结论.
(本小题满分14分) 设函数
设函数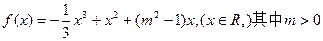 。
。
(Ⅰ)当 曲线
曲线 处的切线斜率(Ⅱ)求函数的单调区间与极值;(Ⅲ)已知函数
处的切线斜率(Ⅱ)求函数的单调区间与极值;(Ⅲ)已知函数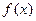 有三个互不相同的零点0,
有三个互不相同的零点0,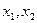 ,且
,且 。若对任意的
。若对任意的 ,
,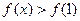 恒成立,求m的取值范围。
恒成立,求m的取值范围。
(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为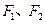 ,离心率
,离心率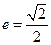 ,右准线方程
,右准线方程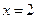 .(1)求椭圆的标准方程;(2)过点
.(1)求椭圆的标准方程;(2)过点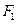 的直线
的直线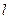 与该椭圆相交于M、N两点,且
与该椭圆相交于M、N两点,且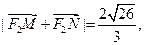 求直线
求直线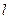 的方程。
的方程。
(本小题满分12分)已知函数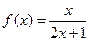 ,数列
,数列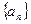 满足
满足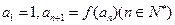 .(Ⅰ)求证:数列
.(Ⅰ)求证:数列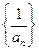 是等差数列;(Ⅱ)记
是等差数列;(Ⅱ)记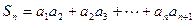 ,试比较
,试比较 与1的大小.
与1的大小.
(本小题满分12分)袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球。(I)试问:一共有多少种不同的结果?请列出所有可能的结果;(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。